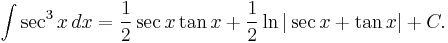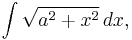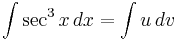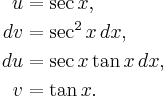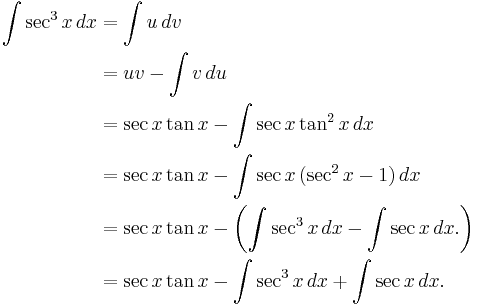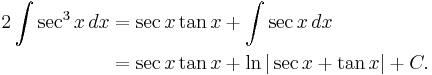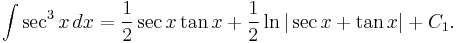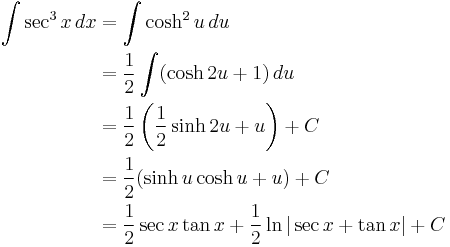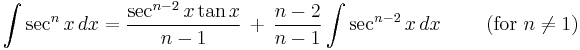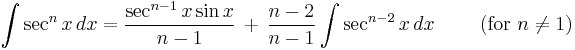Integral of secant cubed

The integral of secant cubed is one of the more challenging^[1] indefinite integrals of elementary calculus:

$\int \sec^3 x \, dx = \frac{1}{2}\sec x \tan x %2B \frac{1}{2}\ln|\sec x %2B \tan x| %2B C.$

There are a number of reasons why this particular antiderivative is worthy of special attention:

The technique used for reducing integrals of higher odd powers of secant to lower ones is fully present in this, the simplest case. The other cases are done in the same way.

The utility of hyperbolic functions in integration can be demonstrated in cases of odd powers of secant (powers of tangent can also be included).

This is one of several integrals usually done in a first-year calculus course in which the most natural way to proceed involves integrating by parts and returning to the same integral one started with (another is the integral of the product of an exponential function with a sine or cosine function; yet another the integral of a power of the sine or cosine function).

This integral is used in evaluating any integral of the form

$\int \sqrt{a^2%2Bx^2}\,dx,$

where a is a constant. In particular, it appears in the problems of:

rectifying (i.e. finding the arc length of) the parabola.
rectifying the Archimedean spiral.
finding the surface area of the helicoid.

1 Derivation
2 Hyperbolic derivation
3 Higher odd powers of secant
4 See also
5 References

Derivation

This antiderivative may be found by integration by parts, as follows:

$\int \sec^3 x \, dx = \int u\,dv$

where

$\begin{align} u &{}= \sec x, \\ dv &{}= \sec^2 x\,dx, \\ du &{}= \sec x \tan x\,dx, \\ v &{}= \tan x. \end{align}$

Then

$\begin{align} \int \sec^3 x \, dx &{}= \int u\,dv \\ &{}= uv - \int v\,du \\ &{} = \sec x \tan x - \int \sec x \tan^2 x\,dx \\ &{}= \sec x \tan x - \int \sec x\, (\sec^2 x - 1)\,dx \\ &{}= \sec x \tan x - \left(\int \sec^3 x \, dx - \int \sec x\,dx.\right) \\ &{}= \sec x \tan x - \int \sec^3 x \, dx %2B \int \sec x\,dx. \end{align}$

Here we have assumed already known the integral of the secant function.

Next we add 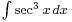$\scriptstyle{}\int\sec^3 x\,dx$ to both sides of the equality just derived:

$\begin{align} 2 \int \sec^3 x \, dx &{}= \sec x \tan x %2B \int \sec x\,dx \\ &{}= \sec x \tan x %2B \ln|\sec x %2B \tan x| %2B C. \end{align}$

Then divide both sides by 2:

$\int \sec^3 x \, dx = \frac{1}{2}\sec x \tan x %2B \frac{1}{2}\ln|\sec x %2B \tan x| %2B C_1.$

Hyperbolic derivation

Integrals of the form: 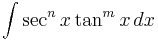$\int \sec^n x \tan^m x\, dx$ can be reduced using the Pythagorean identity if n is even or n and m are both odd. If n is odd and m is even, hyperbolic substitutions can be used to replace the nested integration by parts with hyperbolic power reducing formulas.

$\begin{align} \sec x &{}= \cosh u \\ \tan x &{}= \sinh u \\ \sec^2 x \, dx &{}= \cosh u \, du \text{ or } \sec x \tan x\, dx = \sinh u \, du\\ \sec x \, dx &{}= \, du \text{ or } dx = \operatorname{sech} u \, du \\ u &{}= \operatorname{arcosh} (\sec x ) = \operatorname{arsinh} ( \tan x ) = \ln|\sec x %2B \tan x| \end{align}$

Note that 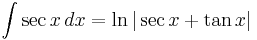$\int \sec x \, dx = \ln|\sec x %2B \tan x|$ follows directly from this substitution.

$\begin{align} \int \sec^3 x \, dx &{}= \int \cosh^2 u\,du \\ &{}= \frac{1}{2}\int ( \cosh 2u %2B1) \,du \\ &{}= \frac{1}{2} \left( \frac{1}{2}\sinh2u %2B u\right) %2B C\\ &{}= \frac{1}{2} ( \sinh u \cosh u %2B u ) %2B C \\ &{}= \frac{1}{2} \sec x \tan x %2B \frac{1}{2} \ln|\sec x %2B \tan x| %2B C \end{align}$

Higher odd powers of secant

Just as the integration by parts above reduced the integral of secant cubed to the integral of secant to the first power, so a similar process reduces the integral of higher odd powers of secant to lower ones. This is the secant reduction formula, which follows the syntax:

$\int \sec^n x \, dx = \frac{\sec^{n-2} x \tan x}{n-1} \,%2B\, \frac{n-2}{n-1}\int \sec^{n-2} x \, dx \qquad \text{ (for }n \ne 1\text{)}\,\!$

Alternatively:

$\int \sec^n x \, dx = \frac{\sec^{n-1} x \sin x}{n-1} \,%2B\, \frac{n-2}{n-1}\int \sec^{n-2} x \, dx \qquad \text{ (for }n \ne 1\text{)}\,\!$

Even powers of tangents can be accommodated by using binomial expansion to form an odd polynomial of secant and using these formulae on the largest term and combining like terms.

References

^ Spivak, Michael (2008). "Integration in Elementary Terms". Calculus. p. 382. "This is a tricky and important integral that often comes up."

Integral of secant cubed

Contents

Derivation

Hyperbolic derivation

Higher odd powers of secant

See also

References